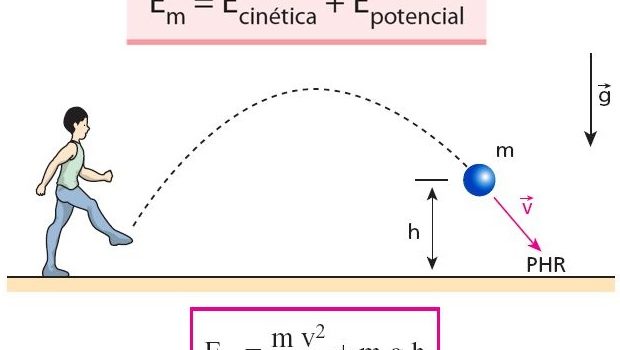
Uma das manifestações mais comuns da energia é a energia mecânica. É sob sua influência que os corpos são postos em movimento, tornando-se possuidores, por sua vez, da mesma modalidade de energia.
Se damos um ponta pé numa bola, esta se movimenta: houve energia mecânica no nosso esforço muscular, enquanto que, deslocando-se, a bola ficou possuída, também, de energia mecânica, capaz, por exemplo, de derrubar uma porção de garrafinhas de madeira. Como se vê, as noções de energia mecânica, força e movimento estão intimamente entrelaçadas.
“A ciência que estuda os movimentos e as forças é a mecânica.”
Movimento na energia mecânica
O movimento é o fenômeno em virtude do qual um corpo ocupa, sucessivamente, diversas posições no espaço. Em outras palavras: um corpo se acha em movimento quando muda de lugar. Em tais condições, as distâncias entre ele e outros corpos, tomadas como pontos de referência, variam com o decorrer do tempo. Podemos, pois, compreender que, se não há variação nessas distâncias, o corpo se acha, ao contrário, em repouso.
Exemplo
Imaginemos um bilhar, tudo preparado para começo de uma partida. Suas três botas se acham em repouso, porque as distâncias entre elas não variam no decorrer do tempo. Tomamos um taco, utilizamos uma força – a força muscular – e impulsionamos, com ele, uma das bolas. Ei-la em movimento, porque, já agora, as distâncias entre ela e as outras duas bolas variam, com o tempo.

Em energia mecânica, o corpo em movimento tem o nome de móvel. E o caminho por ele percorrido se denomina trajetória. Para representá-lo, bastaria unir por uma linha todos os pontos por ele percorridos no espaço.
“Trajetória é a linha seguida por um móvel, durante seu movimento. ”
Trajetória
A trajetória pode ser retilínea e curvilínea. Em consequência, o próprio movimento será retilíneo ou curvilíneo. Neste último caso, pode ser circular (o dos ponteiros de um relógio), elíptico (o da Terra em volta do Sol), etc. Seja retilíneo ou seja curvilíneo, podemos admitir o movimento uniforme e o movimento variado.
Para compreender isso, precisamos de reter, desde logo, a noção de velocidade, que é a relação entre o espaço percorrido por um móvel e o tempo gasto nesse percurso. Ora, movimento uniforme é aquele, em que o móvel percorre espaços iguais em tempos iguais; e movimento variado é aquele em que o móvel percorre espaços iguais em tempos diferentes (ou espaços diferentes em tempos iguais).
Exemplo de trajetória na energia mecânica
Exemplifiquemos. Um automóvel que mantém durante o percurso de dois quilômetros, a mesma velocidade, inalteravelmente, está possuído de um movimento uniforme. Suponhamos que, nessa marcha venceu sessenta quilômetros em uma hora, o que representa um quilômetro por minuto. Trata-se, como se vê, de um movimento uniforme, de uma velocidade constante.

Mas, na prática, o mais comum é o movimento variado. No exemplo dado, o automóvel depara curvas, ladeiras, pontes, obstáculos diversos que o levam a retardar, de vez em quando, a marcha, acelerando-a; em seguida.
Em energia mecânica, o cálculo da velocidade, em tal caso, é o quociente da divisão do percurso total (espaço) pelo tempo total gasto para isso. É o que se chama velocidade média.
Velocidade média
Por exemplo: se em 4 horas, foram percorridos 360 km, a velocidade média foi de 90 km por hora.
No exemplo acima, a velocidade foi calculada em quilômetros por hora. É assim que se calculam as grandes velocidades. Para as pequenas velocidades, o cálculo é feito à base de centímetros por segundo. Por exemplo: a velocidade média de um homem a passo é avaliada em 1.70 m por segundo.
Como vimos linhas atrás, o movimento variado pode acelerar-se ou retardar-se. No movimento acelerado, a velocidade vai crescendo. E, se o acréscimo é igual em tempos iguais, diz-se que o movimento é uniformemente acelerado. Suponha-se que um móvel percorre, em cada segundo, mais um centímetro do que percorreu no segundo anterior.
A sua aceleração é, pois, de 1 cm por segundo. No movimento retardado, a velocidade vai decrescendo. Da mesma forma, se o decréscimo é igual em tempos iguais, o movimento diz-se uniformemente retardado.
Fórmula de velocidade média
A velocidade média é dada pela fórmula:
Aonde:
- Vm= Velocidade média;
= Distância percorrida
= Tempo do percurso.
Movimento periódico e alternativo
Há, ainda, duas modalidades de movimento uniforme na energia mecânica: o periódico e o alternativo. Do primeiro temos exemplo nos diversos ponteiros de um relógio que percorrem inalteravelmente o mesmo espaço em Intervalos iguais de tempo, denominados períodos. Do segundo, o melhor exemplo é o vaivém de uma serra.
Forças na energia mecânica
A noção mais comum que possuímos acerca de força em energia mecânica é a que se relaciona com os músculos, sejam os do nosso corpo, sejam os de um animal que, por exemplo, puxa uma carroça. Partindo daí, passamos a entender como força tudo quanto pode não somente produzir, como modificar, inclusive paralisa; um movimento.
Exemplo
Qualquer jogo de bola nos mostra todas essas modalidades de ação da força muscular: o moinho que gira resulta da força do vento; a locomotiva que se põe em movimento é acionada pela força elétrica ou pela força de compressão do vapor; moléculas de um corpo se aproximam ou se afastam por causa da força de coesão ou da força da repulsão; o corpo que cai porque lhe retiramos os elementos de apoio, cede ao seu piso absoluto, que é uma força de energia mecânica.
Se pendurarmos esse mesmo corpo, o fio que o sustentar representa, igualmente, uma força contrária ao seu piso absoluto (e mais intensa do que ele).
Elementos de força
Os elementos de uma força em energia mecânica são os seguintes:
- Ponto de aplicação direção;
- Sentido;
- Intensidade.
Ponto de aplicação é o ponto material sobre o qual a força atua.
Sentido é a orientação do deslocamento sobre a reta de direção. Para cada direção compreende-se haver dois sentidos. Aliás, o sentido de uma força é sempre indicado por meio de setas. Intensidade é a razão entre a força considerada e uma outra, tomada como unidade.
Direção é a reta que seria gerada pelo ponto de aplicação se iate acompanhasse a solicitação de força.
Exemplo de aplicação de forças na energia mecânica
Voltemos ao exemplo do bilhar e focalizemos uma tacada. Imagine que o jogador aplica a ponta do taco no meio da bola: aí temos, inicialmente, o ponto de aplicação; dada a tacada, a bola segue em determinada direção, provavelmente escolhida pelo jogador.

Repare que dita direção parece um prolongamento, da reta do taco, conto se o ponto de aplicação acompanhasse a solicitação de força. O sentido é dado pela bola, deslocada de um local para outro: a intensidade finalmente, é representada pela grandeza do esforço muscular do jogador.
Intensidade de força
A intensidade de uma força em energia mecânica pode ser medida, teoricamente, pelos efeitos que produz. Estes são de duas ordens: efeitos dinâmicos (produção, modificação, paralisação, de movimentos) e efeitos estéticos (deformação de corpos elásticos impossibilitados de se mover quando submetidos à ação de unia força).
Praticamente a intensidade pode ser medida por meio de aparelhos chamados dinamômetros. São constituídos de molas bastante resistentes cuja flexão ou distensão, provocadas pelos pesos que a elas se penduram, são indicadas num mostrador.
Sistemas de forças
Em energia mecânica, podem as forças ser divididas, quanto à sua duração, em instantes, as que se fazem sentir durante tempo muito curto (uni murro, um choque) e continuas, as que atuam sem interrupção durante todo o tempo em que se opera um movimento ou uma deformação.
Quanto à intensidade, as forças são iguais ou desiguais. Forças iguais são as que possuem a mesma intensidade, produzindo, pois, os mesmos efeitos, sob as mesmas condições. A força única que, resultando delas, for capaz de substituí-las, produzindo iguais efeitos, se denomina resultante.
Quando forças iguais, não paralelas, se aplicam em sentidos contrários, equilibram-se, mantendo imóvel o corpo sobre o qual agem. Forças desiguais são as que possuem intensidades diferentes. A resultante, neste caso, terá o sentido da de maior intensidade.
Resumo: fórmula da energia mecânica
Conforme explicado, a energia mecânica é o resultado da soma da energia cinética e energia potencial. Assim sendo, a fórmula de energia mecânica se dá por:
Em = Ec + EP
Que seriam:
- Em: Energia mecânica;
- Ec: Energia cinética;
- Ep: Energia potencial.
Continue aprendendo com CIÊNCIAS RESUMOS
Gostou desse resumo sobre energia mecânica? Compartilhe!